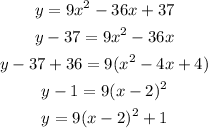Question

All questions relate to the equation y=9 x^2-36 x+37Got it.1. Which way does the parabola open? Your answerYour answerYour answer2. What is the minimum value of y?Your answer3. What is the maximum value of y?Your answer5. What is the axis of symmetry?7. What is the y-intercept?Your answer8. Rewrite the equation in vertex form.

Answer 1

Given the parabola:

`y=9x^2-36x+37`

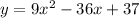
Part 1

To determine the way the parabola opens, we consider the coefficient of x².

• If the coefficient is positive, it opens downwards.

,

• If the coefficient is negative, it opens upwards.

In this case, the coefficient of x²=9 (Positive).

The parabola opens downwards.

Part 2

The minimum value of the parabola occurs at the line of symmetry.

First, we find the equation of the line of symmetry.

`\begin{gathered} x=-(b)/(2a);a=9,b=-36,c=37 \\ \therefore x=-((-36))/(2*9) \\ x=2 \end{gathered}`

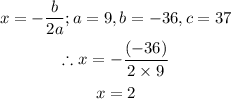
Find the value of y when x=2.

`\begin{gathered} y=9x^2-36x+37 \\ y=9(2)^2-36(2)+37 \\ =36-72+37 \\ Min\text{imum value of y=1} \end{gathered}`

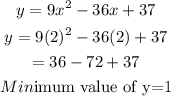
Part 3

Since the graph has a minimum value, the maximum value of y will be ∞.

Part 5

As obtained in part 2 above, the axis of symmetry is:

`x=2`

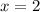
Part 6

The vertex is the coordinate of the minimum point.

At the minimum point, when x=2, y=1.

Therefore, the vertex is (2,1).

Part 7

The y-intercept is the value of y when x=0.

`\begin{gathered} y=9x^2-36x+37 \\ y=9(0)^2-36(0)+37 \\ y=37 \end{gathered}`

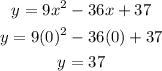
The y-intercept is 37.

Part 8

We rewrite the equation in Vertex form below:

`\begin{gathered} y=9x^2-36x+37 \\ y-37=9x^2-36x \\ y-37+36=9(x^2-4x+4) \\ y-1=9(x-2)^2 \\ y=9(x-2)^2+1 \end{gathered}`