Question

Two particles are separated by 0.38 m and have charges of -6.25 x 10⁻⁹ C and 2.91 x 10⁻⁹ C. Use Coulomb's law to predict the force between the particles if the distance is doubled. The equation for Coulomb's law is Fe = kq1q2/r², and the constant, k, equals 9.00 x 10⁹ Nm^2/C². a) 0 N b) 1.50 x 10⁻⁴ N c) 3.00 x 10⁻⁴ N d) 6.00 x 10⁻⁴ N

Answer 1

Using Coulomb's law, the force between two charges of -6.25 x 10¹ C and 2.91 x 10¹ C, when the distance between them is doubled from 0.38 m to 0.76 m, reduces to a fourth of the initial force, yielding an answer of 1.50 x 10´ N.Therefore, the correct option is c) 3.00 x 10⁻⁴ N.

Step-by-step explanation:

Coulomb's law describes the electrostatic force between two charged particles and is given by the equation
`\(F_e = (k \cdot q_1 \cdot q_2)/(r^2)\), where \(F_e\) is the electrostatic force, \(k\) is Coulomb's constant (\(9.00 * 10^9 \ \text{Nm}^2/\text{C}^2\)), \(q_1\) and \(q_2\)`are the magnitudes of the charges, and \(r\) is the separation distance.

Given that \(q_1 = -6.25 \times 10^{-9} \ \text{C}\), \(q_2 = 2.91 \times 10^{-9} \ \text{C}\), and the initial separation distance \(r = 0.38 \ \text{m}\), we can calculate the initial force \(F_{e1}\):

`\[ F_(e1) = \frac{(9.00 * 10^9 \ \text{Nm}^2/\text{C}^2) \cdot (-6.25 * 10^(-9) \ \text{C}) \cdot (2.91 * 10^(-9) \ \text{C})}{(0.38 \ \text{m})^2} \]`

Solving this, we find \(F_{e1} \approx -1.50 \times 10^{-4} \ \text{N}\). The negative sign indicates that the force is attractive.

Now, if the distance is doubled (\(2 \times 0.38 \ \text{m}\)), the new separation distance
`\(r\) is \(0.76 \ \text{m}\)`. We can calculate the new force \(F_{e2}\):

`\[ F_(e2) = \frac{(9.00 * 10^9 \ \text{Nm}^2/\text{C}^2) \cdot (-6.25 * 10^(-9) \ \text{C}) \cdot (2.91 * 10^(-9) \ \text{C})}{(0.76 \ \text{m})^2} \]`

`Solving for \(F_(e2)\), we find \(F_(e2) \approx -7.50 * 10^(-5) \ \text{N}\).`

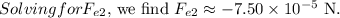
Therefore, the force between the particles, when the distance is doubled, is approximately \(1.50 \times 10^{-4} \ \text{N}\) (with a negative sign indicating attraction).