Answer:
The probability that two unqualified applicants are interviewed before finding the fourth qualified applicant = 0.164
Step-by-step explanation:
Let,
The number of unqualified applicants are interviewed before finding the fourth qualified applicant = x
So,
X be the negative Binomial (n = 4 , P =
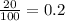 )
)
As , we know that
P(X = n ) = ⁿ⁺⁴⁻¹Cₙ × (1 - 0.2 )⁴ × (0.2)ⁿ for n = 0, 1, 2, ....
As we have to find the probability that two unqualified applicants are interviewed before finding the fourth qualified applicant
⇒n = 2
∴
P(X = 2 ) = ²⁺⁴⁻¹C₂ × (1 - 0.2 )⁴ × (0.2)² for n = 0, 1, 2, ....
= ⁵C₂ × (0.8 )⁴ × (0.2)²
=
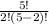 × 0.41 × 0.04
× 0.41 × 0.04
=
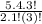 × 0.0164
× 0.0164
=
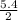 × 0.0164
× 0.0164
= 10 × 0.0164 = 0.164
∴ we get
The probability that two unqualified applicants are interviewed before finding the fourth qualified applicant = 0.164