Question

Consider the following word problem:Two planes, which are 1180 miles apart, fly toward each other. Their speeds differ by 40 mph. If they pass each other in 2 hours, what isthe speed of each?Step 2 of 2: Solve the equation found in Step 1.

Answer 1

To answer this question, we can state the problem as follows:

1. The two planes are 1180 miles apart.

2. They fly toward each other.

3. Their speed differs by 40 mph: that is one of the planes is faster than the other 40 mph, or the other plane is slower than the other plane.

4. The time they encounter each other is 2 hours.

Then, we need to remember the formula for a constant speed:

`V=(d)/(t)`

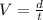
Where

• d is the distance

,

• t is the time

Then, we have that the speeds for each of the planes are:

`V_(p1)=V_(p2)+40`

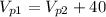
We also have that the sum of the distance for both planes is 1180 miles:

`d_(p1)+d_(p2)=1180`

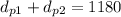
And we have that:

`V=(d)/(t)\Rightarrow d=V\cdot t`
`d_(p1)=V_(p1)\cdot t`
`d_(p2)=V_(p2)\cdot t`

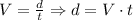
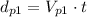
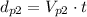
But

`V_(p1)=V_(p2)+40`

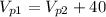
Then, we have that:

`d_(p1)+d_(p2)=1180`
`V_(p1)\cdot t+V_(p2)\cdot t=1180\Rightarrow V_(p1)=V_(p2)+40`
`(V_(p2)+40)\cdot t+V_(p2)\cdot t=1180`

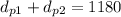
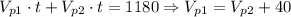
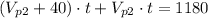
Since t = 2, we have:

`(V_(p2)+40)\cdot2+V_(p2)\cdot2=1180`
`2V_(p2)+80+2V_(p2)=1180\Rightarrow4V_(p2)+80=1180`

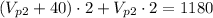
Subtracting 80 from both sides of the equation:

`4V_(p2)+80-80=1180-80\Rightarrow4V_(p2)=1100`

Dividing both sides of the equation by 4, we have:

`V_(p2)=(1100)/(4)\Rightarrow V_(p2)=275\text{mph}`

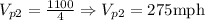
Since we know that:

`V_(p1)=V_(p2)+40`

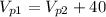
Then, we have:

`V_(p1)=275\text{mph}+40\text{mph}\Rightarrow V_(p1)=315\text{mph}`

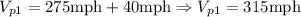
In summary, therefore, the speed of each plane is:

• Speed of Plane 1 = 315 mph

,

• Speed of Plane 2 = 275 mph