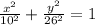The equation of the ellipse is:
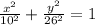
What is the Equation of the Ellipse?
The equation of an ellipse with the foci at (0, 24) and vertices at (0, 26) and (0, -26) can be found using the standard form of the equation of an ellipse, which is:
 .
.
The distance from the center to the foci is the value of (c), and the distance from the center to the vertices is the value of (a).
In this case, the center is at (0, 0), the distance from the center to the foci is 24, and the distance from the center to the vertices is 26.
Therefore, the equation of the ellipse is: