Question

Keep these in unsimplified form.

Answer 1

`\text{(a) } b'(x)= 3\left((x^2)/(x+1)\right)^3 \left(((2x)(x+1)-x^2)/((x+1)^2)\right)\\\\ \\\text{(b) } c'(x)= \frac{2(x^2+3x)^{(1)/(2)}-(2x)((1)/(2)(x^2+3x)^{-(1)/(2)}(2x+3)}{((x^2+3x)^{(1)/(2)})^2}\\\\ \\\text{(c) } d'(x)=(e^x)(\sec^2(x))+(\tan(x))(e^x)`

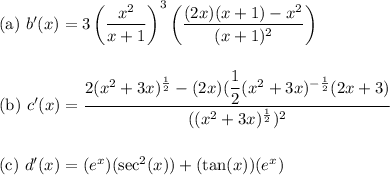
As per request, answers have been left unsimplified.

Explanation:

The task is to determine the derivatives of three given functions, and we will address each one individually. Here are our given functions:

`\text{(a) } b(x)=\left((x^2)/(x+1)\right)^3\\\\ \\\text{(b) } c(x)=(2x)/(√(x^2+3x))\\\\ \\\text{(c) } d(x)=e^x \tan(x)`

`\hrulefill`

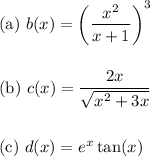
For part (a):

We will apply the power rule, chain rule, and the quotient rule. Here are these rules written out:

`\boxed{\left\begin{array}{ccc}\text{\underline{Power Rule:}}\\\\(d)/(dx)[x^n]=nx^(n-1)\end{array}\right}`

`\boxed{\left\begin{array}{ccc}\text{\underline{The Chain Rule:}}\\\\(d)/(dx)[f(g(x))] =f'(g(x))\cdot g'(x)\end{array}\right}`

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quotient Rule:}}\\\\(d)/(dx)\Big[(f(x))/(g(x)) \Big] = (f'(x)g(x)-f(x)g'(x))/((g(x))^2)\end{array}\right }`

We have,

`\Longrightarrow b(x)=\left((x^2)/(x+1)\right)^3\\\\\\\\(d)/(dx) [b(x)]=(d)/(dx)\left[\left((x^2)/(x+1)\right)^3\right]`

Applying the power rule and chain rule:

`\Longrightarrow b'(x)=3\left((x^2)/(x+1)\right)^3 \cdot (d)/(dx)\left[(x^2)/(x+1)\right]`

To take the derivative of the expression on the far right, use the quotient rule:

`\Longrightarrow b'(x)=3\left((x^2)/(x+1)\right)^3 \cdot \left((((d)/(dx)[x^2])(x+1)-(x^2)((d)/(dx)[x+1]))/((x+1)^2)\right)`

Finishing the derivative we get,

`\therefore b'(x)= \boxed{3\left((x^2)/(x+1)\right)^3 \cdot \left(((2x)(x+1)-x^2)/((x+1)^2)\right)}`

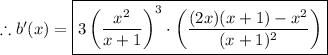
For part (b):

To find the derivative of c(x), first change the square root to a power.

`\Longrightarrow c(x)=(2x)/(√(x^2+3x))\\\\\\\\\Longrightarrow c(x)=\frac{2x}{(x^2+3x)^{(1)/(2)}}\\\\\\\\\Longrightarrow (d)/(dx)[c(x)]=(d)/(dx)\left[\frac{2x}{(x^2+3x)^{(1)/(2)}}\right]`

Now we can use the quotient rule:

`\Longrightarrow c'(x)= \frac{((d)/(dx)[2x])((x^2+3x)^{(1)/(2)})-(2x)((d)/(dx)[(x^2+3x)^{(1)/(2)}])}{((x^2+3x)^{(1)/(2)})^2}`

Use the chain rule to take the derivative of the expression to the 1/2 power:

`\Longrightarrow c'(x)= \frac{2(x^2+3x)^{(1)/(2)}-(2x)((1)/(2)(x^2+3x)^{-(1)/(2)}\cdot(d)/(dx)[x^2+3x])}{((x^2+3x)^{(1)/(2)})^2}`

Finishing the derivative, we get:

`\therefore c'(x)= \boxed{ \frac{2(x^2+3x)^{(1)/(2)}-(2x)((1)/(2)(x^2+3x)^{-(1)/(2)}\cdot(2x+3)}{((x^2+3x)^{(1)/(2)})^2}}`

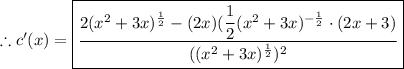
For part (c):

To differentiate d(x) we will use the following rules:

`\boxed{\left\begin{array}{ccc}\text{\underline{Product Rule:}}\\\\(d)/(dx)[f(x)g(x)]=f(x)g'(x)+g(x)f'(x) \end{array}\right }`

`\boxed{\left\begin{array}{ccc}\text{\underline{Exponetial Rule:}}\\\\ (d)/(dx)[e^x]=e^x\end{array}\right}`

`\boxed{\left\begin{array}{ccc}\text{\underline{Tangent Rule:}}\\\\ (d)/(dx)[\tan(x)]=\sec^2(x)\end{array}\right}`

Start by using the product rule:

`\Longrightarrow d(x)=e^x \tan(x)\\\\\\\\\Longrightarrow (d)/(dx) [d(x)]=(d)/(dx) [e^x \tan(x)]\\\\\\\\\Longrightarrow d'(x)=(e^x)((d)/(dx) [\tan(x)])+(\tan(x))((d)/(dx) [e^x])`

Now applying the exponential rule and tangent rule:

`\therefore d'(x)=\boxed{(e^x)(\sec^2(x))+(\tan(x))(e^x)}`

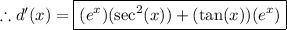
Thus, all derivatives have been found. None have been simplified as per your request.