Answer:
The average rate of change of the height over the interval [1, 2.5] is - 56 feet per second.
Explanation:
Let
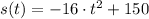 . Geometrically speaking, average rate of change over a given interval (
. Geometrically speaking, average rate of change over a given interval (
 ), measured in feet per second, is determined by definition of secant line, which is defined:
), measured in feet per second, is determined by definition of secant line, which is defined:
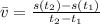 (1)
(1)
Where:
 ,
,
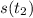 - Initial and final position of the object, measured in feet.
- Initial and final position of the object, measured in feet.
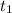 ,
,
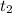 - Initial and final times, measured in seconds.
- Initial and final times, measured in seconds.
If we know that
 and
and
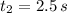 , then the average rate of change over the interval
, then the average rate of change over the interval
![[1,2.5]](https://img.qammunity.org/2022/formulas/mathematics/high-school/poyw49wbndc9sbypgtwsdh6xl50pcsbwrs.png) :
:

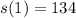
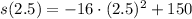

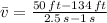
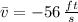
The average rate of change of the height over the interval [1, 2.5] is - 56 feet per second.