Question

A farmer has 1,416 feet of fencing available to enclose a rectangle area bordering a river. No fencing is required along the river. Let x represent the length of the side of the rectangular enclosure that is perpendicular A(x)= Find the dimensions that will maximize the area. The length of the side rectangle perpendicular to the river is and the length of the side of the rectangle parallel to the river is.What is the maximum area?

Answer 1

Answer:

The dimensions that will maximize the area are x = 354 ft and y = 708 ft

The length of the side rectangle perpendicular to the river is 354 ft

The length of the side of the rectangle parallel to the river is 708 ft

The maximum area = 250632 ft²

Step-by-step explanation:

Given:

The length of the fencing = 1416 ft

The length of the side rectangle perpendicular to the river = x

To find:

The dimensions that will maximize the area

To determine the dimensions, we will make an illustration of the given information:

let the length o the rectangle parallel to the river = y

Length of the for the enclosed area = Perimeter of the enclosed area

Perimeter of the enclosed area = x + x = y = 2x + y

`1416=2x+y\text{ . . .\lparen1\rparen}`

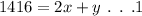
Area of the rectangle = length × width

length = y, width = x

let the Area of the rectangle = A(x)

`A(x)\text{ = xy . . . \lparen2\rparen}`

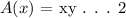
To get the expression for A(x), we will make y the subject of the formula in equation (1):

y = 1416 - 2x

substitute for y in equation (2):

`\begin{gathered} A(x)\text{ = x\lparen1416 - 2x\rparen} \\ \\ A(x)\text{ = 14166x - 2x}^2 \end{gathered}`

To get the maximum dimension, we will differentiate with respect to x:

`\begin{gathered} A^(\prime)(x)\text{ = 1416 - 4x} \\ \\ At\text{ maximum, A'\lparen x\rparen = 0:} \\ 1416\text{ - 4x = 0} \\ 1416\text{ = 4x} \\ x\text{ = }(1416)/(4) \\ x\text{ = 354} \end{gathered}`

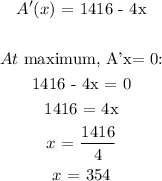
substitute for x in equation (1):

`\begin{gathered} 1416\text{ = 2\lparen354\rparen + y} \\ 1416\text{ - 708 = y} \\ y\text{ = 708} \end{gathered}`

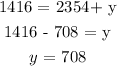
The dimensions that will maximize the area are x = 354 ft and y = 708 ft

The length of the side rectangle perpendicular to the river is 354 ft

The length of the side of the rectangle parallel to the river is 708 ft

The maximum area = 354 × 708

The maximum area = 250632 ft²