Initially, Sudeep and Michael had 150 and 70 sweets, respectively.
How to find how many sweets did they have initially
Let's the initial number of sweets that Sudeep and Michael have as 15x and 7x respectively
After giving Michael 36 sweets, his new amount becomes (7x + 36), and the ratio becomes 3:19.
So, we can set up the equation:
 =
=
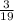
Now, cross-multiplying to solve for x
15x * 19 = 3 * (7x + 36)
285x = 21x + 108
By Subtracting 21x from both sides:
264x = 108
Now, divide by 264 to find x
x =
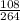
Lets multiply by the initial amounts to find the total number of sweets:
15x * 7 + 7x = 15 *
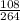 * 7 + 7 *
* 7 + 7 *
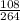
![\[15 * (108)/(264) * 7 + 7 * (108)/(264)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zzznpq7gglwrq99qjy5dgtd99gi5lb2jif.png)
![\[ (15 * 108 * 7)/(264) + (7 * 108)/(264)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/azqga4g47wtn83skyxeis32ish98on9jwy.png)
=
![\[ (1890 + 756)/(264)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fmug6p3sedjn4idm4hahhuqz16rciwv3ky.png)
=
![\[ (2646)/(264)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yzxh55aa0bvm9pa0k4snfuhkpdc9ewc8kx.png)
= 10
Therefore, initially, Sudeep and Michael had 15 * 10 = 150 and 7 * 10 = 70 sweets, respectively.