Question

Write the following parametric equations as a polar equation.x = 2ty=t²

Answer 1

2nd option: r = 4 tan θ sec θ

Explanation:

We have the following:

`\begin{gathered} x=2t\rightarrow t=(x)/(2) \\ \\ y=t^2 \end{gathered}`

We substitute the first equation in the second and we are left with the following:

`\begin{gathered} y=\left((x)/(2)\right)^2 \\ \\ y=(x^2)/(2^2)=(x^2)/(4) \end{gathered}`

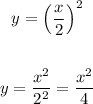
Now, we convert this to polar coordinates, just like this:

`\begin{gathered} x=r\cos\theta,y=r\sin\theta \\ \\ \text{ We replacing:} \\ \\ r\sin\theta=((r\cos\theta)^2)/(4) \\ \\ r\sin\theta=\frac{r^2\cos^2\theta^{}}{4} \\ \\ r\sin\theta=\frac{r^2\cos\theta\cdot\cos\theta{}}{4} \\ \\ (r^2\cos\theta\cdot\cos\theta)/(4)=r\sin\theta \\ \\ r=4(\sin\theta)/(\cos\theta)\cdot(1)/(\cos\theta) \\ \\ r=4\tan\theta\cdot\sec\theta \end{gathered}`

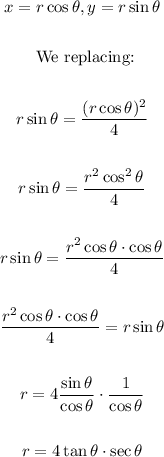
So the correct answer is the 2nd option: r = 4 tan θ sec θ