To answer this question we first need to notice that the sequence of dots increases by a factor of 3 in each drawing. This means that this is a geometric sequence with common ratio 3.
We know that the nth term of a geometric sequence is given by:
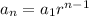
where a1 is the first term and r is the common ratio. In this case a1=3 and r=3, hence the nth term is:
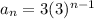
Now, if we add the first 15 stages, this means that we are adding the first 15 terms of the sequence, then our sum will be of the form:

Then we notice that option a is a correct expression for the sum of the first 15 stages.
We also know that the sum of the first nth terms of a geometric sequence is given by:
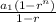
plugging the values we know, we have that:
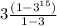
Therefore option d is also a correct expression for the sum of the first 15 stages.