Question

A polling company is trying to estimate the percentage of adults that consider themselves happy. A confidence interval based on a sample size of 180 has a larger than desired margin of error. The company wants to conduct another poll and obtain another confidence interval of the same level but reduce the error to one-third the size of the original sample. How many adults should they now interview

Answer 1

They should interview 1620 adults now.

Explanation:

Margin of error of a confidence interval:

The margin of error of a confidence interval has the following format:

`M = z(\sigma)/(√(n))`

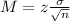
In which z is related to the confidence level,
`\sigma` is the standard deviation of the population and n is the size of the sample.

In this question:

z wont change, neither will
`\sigma`

We want to increase n as such the margin of error is reduced to one third.

We have that the margin of error is inversely proportional to the square root of the size of the sample, which means that for the margin of error to be reduced to one third, the sample size has to be multiplied by
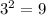`3^2 = 9`. So

180*9 = 1620

They should interview 1620 adults now.