Question

the quantity , in grams, of a certain radioactive substance decreases according to the exponential decay model , where is measured in seconds. during an experiment, a scientist determines that the rate of decay of a second substance with the quantity , in grams, can be represented by a linear model , where is measured in seconds. if at time , and , at what time , in seconds, will there be equal quantities of both substances? responses

Answer 1

At time t ≈ 6.329 seconds, there will be equal quantities of both substances. C

How to determine the time when there are equal quantities of both substances

To determine the time t when there are equal quantities of both substances, solve the equation:

R(t) = S(t)

Substituting the given exponential decay model for R(t) and the linear model for S(t), we get:

0.05R₀
`e^(`-0.05t) = 4t - 20

Where R₀ is the initial quantity of the radioactive substance (R₀ = 100 grams).

To solve for t, first solve for R₀
`e^(`-0.05t) by dividing both sides of the equation by 0.05:

R₀
`e^(`-0.05t) = 80t - 400

Then, we can substitute R₀ with its initial value:

100
`e^(-`0.05t) = 80t - 400

Next, rewrite the exponential term as a power of e:

`(e^(-0.05))^(t) = 80t - 400`

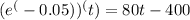
Taking the natural logarithm of both sides

-0.05t = ln(80t - 400)

Solving for t using numerical methods

t ≈ 6.329

Therefore, at time t ≈ 6.329 seconds, there will be equal quantities of both substances.

The quantity R, in grams, of a certain radioactive substance decreases according to the exponential decay model R = 0.05R, where R is measured in seconds. During an experiment, a scientist determines that the rate of decay of a second substance with the quantity S, in grams, can be represented by the linear model d5 ~4_, where S is measured in seconds. If at time t = 0, R(0) = 100 and S(0) = 125, at what time t, in seconds, will there be equal quantities of both substances?

A. t = 31.197

B. t = 23.548

(C) t = 6.329

(D) t = 6318