Question

1277 concert tickets were sold for a total of $16,267. If students paid $11 and nonstudents paid $17, how manystudent tickets were sold?

Answer 1

Hello there. To solve this question, we'll have to remember some properties about system of equations.

Given that 1277 concert tickets were sold, for a total of $16,267, knowing that students paid $11 and non-students paid $17, we have to determine how many students tickets were sold.

Let's start labeling the variables we have. Say x is the number of tickets sold for students, while y is the number of tickets sold for non-students.

The total number of tickets sold can be found by adding how many students and non-students tickets were sold, i.e.

`x+y=1277`

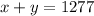
To find the total amount collected, we have to multiply the number of each ticket sold by its respective fee, adding everything as follows:

`11\cdot x+17\cdot y=16267`

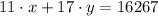
With this, we have the following system of equations:

`\begin{cases}x+y=1277 \\ 11x+17y=16267\end{cases}`

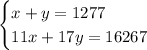
We can solve it using the elimination method. It consists in multiplying any of the equations by a factor (usually the easier equation) that when added to the other equation, one of the variables are cancelled out.

In this case, multiply the first equation by a factor of (-11)

`\begin{cases}-11x-11y=-14047 \\ 11x+17y=16267\end{cases}`

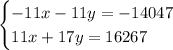
Add the two equations

`\begin{gathered} -11x-11y+11x+17y=-14047+16267 \\ 6y=2220 \end{gathered}`

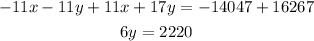
Divide both sides by a factor of 6

`y=370`

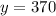
Now we plug it back into the first equation in order to solve for x (i. e the number of tickets sold for students)

`\begin{gathered} x+y=1277 \\ x+370=1277 \\ x=1277-370 \\ x=907 \end{gathered}`

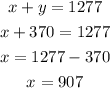
This is how many tickets were sold to students.