To have a 96% probability of accommodating all of the waiting cars, the new bank should provide at least 6 spaces for cars waiting for drive-up teller service.
How to find probability?
To determine the number of spaces needed to accommodate all of the waiting cars with a 96% probability, we can use the M/M/c queuing model.
The arrival rate is given as 36 customers per hour. Since we want the arrival rate in customers per minute, we convert it as follows:
Arrival rate (λ) = 36 customers/hour ÷ 60 minutes/hour
= 0.6 customers/minute
The service rate is given as 4 minutes per customer. To know the service rate in customers per minute, convert it as follows:
Service rate (μ) = 1 customer ÷ 4 minutes/customer
= 0.25 customers/minute
The traffic intensity (ρ) is the ratio of the arrival rate to the service rate:
ρ = λ/μ
= 0.6 customers/minute ÷ 0.25 customers/minute
= 2.4
For a 96% probability of accommodating all of the waiting cars, we need to find the number of spaces (c) such that the Erlang-B formula (B(c, ρ)) is equal to 0.96.
B(c, ρ) = 1 - (ρ/c)
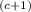 / (c! × (1 + ρ/c)
/ (c! × (1 + ρ/c)
 )
)
Plugging in the values:
0.96 = 1 - (2.4/c)
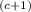 / (c! × (1 + 2.4/c)
/ (c! × (1 + 2.4/c)
 )
)
This equation can be solved using numerical methods, such as trial and error or a spreadsheet program. The solution is c ≈ 5.1.
Therefore, to have a 96% probability of accommodating all of the waiting cars, the new bank should provide at least 6 spaces for cars waiting for drive-up teller service.