Question

A car of mass m rests at the top of a hill of height h before rolling without friction into a crash barrier located at the bottom of the hill. the crash barrier contains a spring with a spring constant k, which is designed to bring the car to rest with minimum damage, determine, in terms of m, h, k and g, the maximum distance (x) the spring will be compressed when the car hits it?

Answer 1

`\displaystyle x = \sqrt{(2\, m\, g\, h)/(k)}`.

Step-by-step explanation:

Consider how energy is converted during this motion:

• while the vehicle is rolling down the hill, gravitational potential energy (
  `\text{GPE}`) would be converted into kinetic energy (
  `\text{KE}`);
• while the spring is slowing the vehicle down, kinetic energy (
  `\text{KE}`) of the vehicle would be converted into the elastic potential energy (
  `\text{EPE}`) of the spring.

Under the assumptions, total mechanical energy of this system would be conserved. Hence, the elastic potential energy that the spring gained would be equal to the change in the initial gravitational potential energy of the vehicle:

`(\text{EPE}) = (\text{change in GPE})`.

The elastic potential energy stored in an ideal spring is:

`\displaystyle (\text{EPE}) = (1)/(2)\, k\, x^(2)`,

Where:

• 
  `k` is the spring constant, and
• 
  `x` is the displacement of the spring from the equilibrium position.

In a gravitational field of uniform strength
`g`, the change in the gravitational potential energy of an object is:

`(\text{change in GPE}) = m\, g\, h`,

Where:

• 
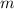  `m` is the mass of the object,
• 
  `g` is the strength of the gravitational field, and
• 
  `h` is the change in the altitude of the object (displacement in the direction opposite to the gravitational attraction.)

Assume that when the vehicle comes into contact with the spring, the additional height change from the displacement of the spring
`x` is negligible relative to the height of the hill,
`h`.

Solve the equation
`(\text{EPE}) = (\text{change in GPE})` for the displacement of the spring,
`x`:

`\displaystyle (1)/(2)\, k\, x^(2) = m\, g\, h`.

`\begin{aligned}x &= \sqrt{(2\, m\, g\, h)/(k)}\end{aligned}`.

In other words, the maximum possible compression of the spring would be
`√((2\, m\, g\, h) / k)` under the assumptions.