Question

I'm not sure how to fill this problem in (a) Find the general solution of the given system of equations. \[ \mathbf{x}^{\prime}=\left(\begin{array}{cc} 4 & -10 \\ 3 & -7 \end{array}\right) \mathbf{x} \] \[ \mathbf{x}(t)=c_{1} \mid \quad+c_{2

Answer 1

The general solution of the given system of differential equations is
`\[ \mathbf{x}(t) = c_1 \begin{bmatrix} 2 \\ 3 \end{bmatrix} e^(-t) + c_2 \begin{bmatrix} 5 \\ 1 \end{bmatrix} e^(-3t) \]`, where
`\(c_1\)` and
`\(c_2\)` are arbitrary constants.

Step-by-step explanation:

To find the general solution, we start by solving the characteristic equation of the coefficient matrix. The characteristic equation is obtained by setting the determinant of the matrix
`\(A - \lambda I\)` equal to zero, where (A) is the coefficient matrix,
`\(\lambda\)` is the eigenvalue, and (I) is the identity matrix.

For the given matrix
`\[ A = \begin{bmatrix} 4 & -10 \\ 3 & -7 \end{bmatrix} \],` the characteristic equation is
`\(det(A - \lambda I) = 0\).` Solving this equation yields two distinct eigenvalues:
`\(\lambda_1 = -1\) and \(\lambda_2 = -3\).`

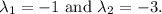
Next, we find the corresponding eigenvectors by solving the system
`\((A - \lambda I) \mathbf{v} = 0\)` for each eigenvalue. The eigenvectors associated with
`\(\lambda_1 = -1\) and \(\lambda_2 = -3\)` are
`\(\begin{bmatrix} 2 \\ 3 \end{bmatrix}\)` and
`\(\begin{bmatrix} 5 \\ 1 \end{bmatrix}\)`, respectively.

Finally, we combine the eigenvalues and eigenvectors into the general solution
`\[ \mathbf{x}(t) = c_1 \begin{bmatrix} 2 \\ 3 \end{bmatrix} e^(-t) + c_2 \begin{bmatrix} 5 \\ 1 \end{bmatrix} e^(-3t) \],`where
`\(c_1\)` and
`\(c_2\)` are arbitrary constants determined by initial conditions if provided. This solution represents the linear combination of the eigenvectors scaled by the corresponding exponential terms, providing a complete description of the system's behavior over time.