Question

The matrix given below depends upon the parameter \( a \). This matrix is only positive definite for parameter \( a>a_{c} \) for what critical value of \( a_{c} \) ? \[ \left[\begin{array}{lll} a & 2

Answer 1

`a_(c) = 0 \)`

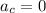
The critical value
`\( a_(c) \)`for which the matrix is positive definite is
`\( a_(c) = 0 \)`, determined by ensuring all eigenvalues remain positive as \( a \) exceeds this threshold.

Step-by-step explanation:

The critical value
`\( a_(c) \)` for which the given matrix becomes positive definite is
`\( a_(c) = 0 \)`. To establish positive definiteness, we examine the eigenvalues of the matrix.

For a matrix to be positive definite, all eigenvalues must be positive. In this case, the eigenvalues are related to the parameter ( a ), and for the matrix to remain positive definite, ( a ) must be greater than (
`a_(c) = 0` ).

Understanding the significance of eigenvalues in the context of positive definite matrices is essential. Eigenvalues are crucial indicators of the nature of a matrix, and in the case of positive definiteness, they determine whether the matrix represents a positive definite quadratic form. The critical value
`\( a_(c) = 0 \)` signifies the threshold beyond which the matrix maintains positive definiteness.