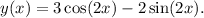Final Answer
The solution to the given differential equation with the specified initial conditions is
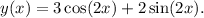
Step-by-step explanation
To solve the differential equation
 we first find the complementary solution to the homogeneous equation \y'' + 6y + 9y = 0 . The characteristic equation is
we first find the complementary solution to the homogeneous equation \y'' + 6y + 9y = 0 . The characteristic equation is
 which factors to
which factors to
 This gives a repeated root r = -3 . The complementary solution is then
This gives a repeated root r = -3 . The complementary solution is then
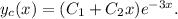
Next, we find the particular solution for the non-homogeneous part
 , we substitute it into the differential equation and solve for the coefficients A and B. The particular solution is
, we substitute it into the differential equation and solve for the coefficients A and B. The particular solution is
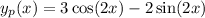
Combining the complementary and particular solutions, we get the general solution
 Applying the initial conditions
Applying the initial conditions
 Therefore, the final solution is
Therefore, the final solution is