Question

In each part, determine all values of \( p \) for which the integral is improper. Enter in interval notation or "none" if there are no relevant values of \( p \). (a) \( \int_{0}^{6} \frac{d x}{x ?} \

Answer 1

The integral
`\( \int_(0)^(6) (1)/(x^p) \, dx \)` is improper when
`\( p \leq 0 \)` and
`\( p \\eq 1 \).`

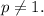
Step-by-step explanation:

The given integral
`\( \int_(0)^(6) (1)/(x^p) \, dx \)`is improper when the power
`\( p \)` in the denominator leads to convergence issues. For an integral to be proper, it should converge to a finite value.

If
`\( p \leq 0 \)`, the integral is improper because it involves division by zero when
`\( x = 0 \)`. In this case, the function is not defined at \( x = 0 \), leading to a singularity and making the integral improper.

Additionally, when
`\( p = 1 \),` the integral is improper due to the presence of a logarithmic singularity at
`\( x = 0 \)`. The logarithmic singularity causes the integral to diverge.

For all other values of
`\( p \)`, the integral is proper and converges within the given limits of integration (0 to 6). Therefore, the final answer is that the integral is improper when
`\( p \leq 0 \)` and
`\( p \\eq 1 \)`.