Final Answer:
The population of Franklin, years after the employer left town, can be modeled by the exponential decay equation
 where P
where P
 is the population after t years,
is the population after t years,
 is the initial population, and k is the decay constant. For this specific scenario, the equation is
is the initial population, and k is the decay constant. For this specific scenario, the equation is
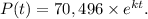
Step-by-step explanation:
The given information states that after 3 years, the population was 70,496, and after 4 years, it was 62,742. We can use these data points to determine the decay constant k. When t = 3, P(3) = 70,496, and when t = 4, P(4) = 62,742.
Substitute these values into the equation:
![\[70,496 = P_0 * e^(3k)\]](https://img.qammunity.org/2024/formulas/mathematics/college/1rzpl5yhp16ofh85a65kar4v42o0yxck7w.png)
![\[62,742 = P_0 * e^(4k)\]](https://img.qammunity.org/2024/formulas/mathematics/college/hbk9ediyxrca1ihj1manezfd29vbx7191g.png)
Now, divide the two equations to eliminate
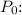
![\[(70,496)/(62,742) = (e^(3k))/(e^(4k))\]](https://img.qammunity.org/2024/formulas/mathematics/college/v4imijjz8friwh0pdy4fz8xiqcyb8yifcl.png)
Simplify the expression on the right side:
![\[(70,496)/(62,742) = e^(-k)\]](https://img.qammunity.org/2024/formulas/mathematics/college/q76efoeuyl62vq3og2tcgzxhr52jpe4fbd.png)
Now, solve for k:
![\[e^(-k) = (70,496)/(62,742)\]](https://img.qammunity.org/2024/formulas/mathematics/college/genomhz8ptkqsydbw4odp2ka141bn9kllb.png)
Take the natural logarithm (ln) of both sides:
![\[-k = \ln\left((70,496)/(62,742)\right)\]](https://img.qammunity.org/2024/formulas/mathematics/college/8qvbyr7klowgo55my0musj9mswq90rmadv.png)
Finally, solve for k:
![\[k = -\ln\left((70,496)/(62,742)\right)\]](https://img.qammunity.org/2024/formulas/mathematics/college/sh1th1xexmnx8lwoxvro227l6gregyliqc.png)
Now that we have k, we can use it in the exponential decay equation
 to model the population of Franklin for any given time t after the employer left town.
to model the population of Franklin for any given time t after the employer left town.