Question

A curve is given by x=t³+3t+1,y=t³−12t²+21t. Which one of the following describes the entire set of t values where the curve is decreasing? (A) (−1,1) (B) No such t exists (C) (−[infinity],−1)(1,[infinity]) (D) (1,7) (E) (0,1)(7,[infinity]) (F) (−[infinity],0)(1,7) (G) All possible t-values (H) (−[infinity],1)(7,[infinity])

Answer 1

The curve described by
`\(x = t^3 + 3t + 1\)` and
`\(y = t^3 - 12t^2 + 21t\)` is decreasing in the interval 1 < t < 7. Therefore, the answer is (1,7).

(D) (1,7).

Step-by-step explanation:

To find where the curve is decreasing, we need to examine the behavior of the derivative of y with respect to t, which is dy/dt. If dy/dt is negative over a certain interval, it means that y is decreasing over that interval.

Let's find dy/dt:

`\( x = t^3 + 3t + 1 \\`

`\( y = t^3 - 12t^2 + 21t \\`

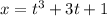
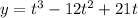
Now, find
`\((dy)/(dt)\)`:

`\( (dy)/(dt) = (d)/(dt)(t^3 - 12t^2 + 21t) \\`

`\( (dy)/(dt) = 3t^2 - 24t + 21 \\`

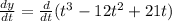
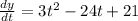
To find where the curve is decreasing, we want to find the values of t for which
`\((dy)/(dt) < 0\)`. Solve the inequality:

`\[ 3t^2 - 24t + 21 < 0 \]`

Factoring the quadratic, we get:

`\[ (t - 1)(3t - 21) < 0 \]`

Solving for t, we find two critical points: t = 1 and t = 7.

Now, we can test intervals around these critical points to determine where the inequality is satisfied.

- For t < 1, both factors are negative, so the product is positive.

- For 1 < t < 7, the first factor is positive, and the second factor is negative, so the product is negative.

- For
`\(t > 7\)`, both factors are positive, so the product is positive.

Therefore, the curve is decreasing for
`\(1 < t < 7\)`.

Now, let's check the answer choices:

The correct answer is (D) (1,7).