Question

Evaluate the piecewise defined function for the given values of x.F(x)= -x -1 for x<-1, -3 for -1≤x<2, √x-2 for x≥2A. f(-3)B. f(-1)C. f(2)D. f(6)

Answer 1

`\begin{gathered} f(-3)=2 \\ f(-1)=-3 \\ f(2)=0 \\ f(6)=2 \end{gathered}`

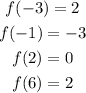
Step-by-step explanation:

Given the piecewise defined function;

`f(x)=\mleft\{\begin{aligned}-x-1for\rightarrow x<-1_{} \\ -3\text{for} \\ \sqrt[]{x-2}\text{ for}\rightarrow x\ge2\end{aligned}\mright.\rightarrow-1\leq x<2`

a) f(-3)

we want to find the value of f(x) at x=-3.

-3 is less than -1, so it falls within the interval x<-1.

`\begin{gathered} f(x)=-x-1 \\ f(-3)=-(-3)-1 \\ f(-3)=3-1 \\ f(-3)=2 \end{gathered}`

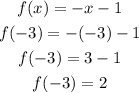
b) f(-1)

-1 falls with the second interval

`-1\leq x\leq2`

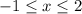
For this interval, f(x) is always equal to -3.

`\begin{gathered} f(x)=-3 \\ f(-1)=-3 \end{gathered}`

c) f(2)

2 falls within the last interval.

`\begin{gathered} f(x)=\sqrt[]{x-2} \\ f(2)=\sqrt[]{2-2} \\ f(2)=0 \end{gathered}`

d) f(6)

6 falls within the last interval.

`\begin{gathered} f(x)=\sqrt[]{x-2} \\ f(6)=\sqrt[]{6-2} \\ f(6)=\sqrt[]{4} \\ f(6)=2 \end{gathered}`