Question

Suppose S is a σ-algebra on a set X and A⊂X. Let Sₐ ={E∈S:A⊂E or A∩E=∅} (a) Prove that Sₐ is a σ-algebra on X. (b) Suppose f:X→R is a function. Prove that f is measurable with respect to Sₐ if and only if f is measurable with respect to S and f is constant on A.

Answer 1

(a)
`\(S_A\) is a \(\sigma\)-algebra on \(X\)`.

(b)
`\(f\)` is measurable with respect to
`\(S_A\`) if and only if
`\(f\)` is measurable with respect to
`\(S\) and \(f\) is constant on \(A\).`

Step-by-step explanation:

(a) To prove that
`\(S_A\)` is a
`\(\sigma\)-algebra on \(X\)`, we need to show that
`\(S_A\)`satisfies the three properties of a
`\(\sigma\)-algebra`: closure under complements, closure under countable unions, and closure under countable intersections.

Closure under complements: For any
`\(E \in S_A\), either \(A \subset E\) or \(A \cap E = \emptyset\). Thus, \(A^c \subset E^c\) or \(A^c \cap E^c = \emptyset\), implying that \(E^c \in S_A\).`

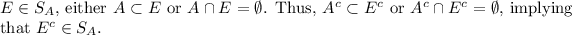
Closure under countable unions: If
`\(E_1, E_2, \ldots \in S_A\)`, then for each
`\(i\), either \(A \subset E_i\) or \(A \cap E_i = \emptyset\).` Taking the union, we get
`\(A \subset \bigcup_i E_i\) or \(A \cap \bigcup_i E_i = \emptyset\), implying \(\bigcup_i E_i \in S_A\).`

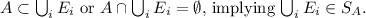
Closure under countable intersections: Similarly, if
`\(E_1, E_2, \ldots \in S_A\)`, then for each
`\(i\)`, either
`\(A \subset E_i\) or \(A \cap E_i = \emptyset\)`. Taking the intersection, we get
`\(A \subset \bigcap_i E_i\) or \(A \cap \bigcap_i E_i = \emptyset\), implying \(\bigcap_i E_i \in S_A\).`

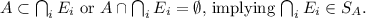
(b) To prove the second statement, we need to show both directions: (i) if
`\(f\)`is measurable with respect to
`\(S_A\)`, then it is measurable with respect to
`\(S\) and constant on \(A\), and (ii) if \(f\)` is measurable with respect to
`\(S\)` and constant on
`\(A\)`, then it is measurable with respect to
`\(S_A\)`.

These proofs involve demonstrating that the pre-image of any Borel set under
`\(f\)` satisfies the required conditions, establishing the desired measurability properties.