Question

Compute the line integral of the vector field F(x,y,z)=⟨4ex,yez,7⟩ over the closed curve C which consists of line segments from (0,0,0) to (0,3,0) to (5,3,5) to (5,0,5) to (0,0,0)

Answer 1

The line integral of the vector field
`\( \mathbf{F}(x,y,z) = \langle 4e^x, y e^z, 7 \rangle \)`over the closed curve
`\( C \) is \( 75e^5 - 21 \).`

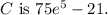
Step-by-step explanation:

This line integral involves evaluating the vector field \
`( \mathbf{F} \) \( \mathbf{F}(x,y,z) = \langle 4e^x, y e^z, 7 \rangle \)`along the given closed curve \
`( C \)`consisting of line segments connecting specific points in 3D space. The line integral is computed by parameterizing each segment of the curve, calculating the dot product of the vector field
`\( \mathbf{F} \)` with the differential length element, and then integrating over each segment.

Initially, the integral is solved by integrating along the line segment from (0,0,0) to (0,3,0), then from (0,3,0) to (5,3,5), followed by the segment from (5,3,5) to (5,0,5), and finally from (5,0,5) back to the starting point at (0,0,0). Each segment's integral involves plugging in the parametric equations for the curve segments and evaluating the dot product of \
`( \mathbf{F} \)`with the tangent vector, integrating with respect to the parameter, and summing up these contributions over all segments.

The final result of
`\( 75e^5 - 21 \)`is obtained after carrying out the calculations for each segment's line integral and summing these values together.