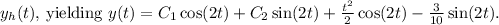Final answer:
The general solution to the non-homogeneous equation is then obtained by summing the particular solution
 with the general solution of the homogeneous equation
with the general solution of the homogeneous equation

Step-by-step explanation:
The given second-order linear homogeneous differential equation
 is solved by employing the method of undetermined coefficients. First, the general solution of the associated homogeneous equation
is solved by employing the method of undetermined coefficients. First, the general solution of the associated homogeneous equation
 is found to be
is found to be
 are arbitrary constants.
are arbitrary constants.
To solve for the particular solution, the right-hand side of the non-homogeneous equation
 is broken down into two parts:
is broken down into two parts:
 Assuming a particular solution in the form
Assuming a particular solution in the form
 is substituted into the differential equation.
is substituted into the differential equation.
By equating coefficients and solving the resulting system of equations, the particular solution is found to be
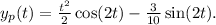
The general solution to the non-homogeneous equation is then obtained by summing the particular solution
 with the general solution of the homogeneous equation
with the general solution of the homogeneous equation