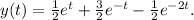Final Answer:
The solution to the given differential equation is
 are constants determined by the initial conditions.
are constants determined by the initial conditions.
Step-by-step explanation:
The given differential equation
 is a third-order linear homogeneous differential equation. The general solution to such an equation is a linear combination of the complementary solutions. In this case, the complementary solutions are
is a third-order linear homogeneous differential equation. The general solution to such an equation is a linear combination of the complementary solutions. In this case, the complementary solutions are
 based on the characteristic equation.
based on the characteristic equation.
The general solution is given by
 are constants to be determined. To find these constants, we use the initial conditions
are constants to be determined. To find these constants, we use the initial conditions
 Evaluating these conditions gives a system of three equations. Solving this system, we find
Evaluating these conditions gives a system of three equations. Solving this system, we find
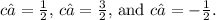
Substituting these values back into the general solution, we get the particular solution
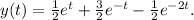 Therefore, the final answer is
Therefore, the final answer is