Question

Find a particular solution to the following differential equation using the method of variation of parameters.

Answer 1

The particular solution to the given differential equation using the method of variation of parameters is y_p(x) = -
`x^2e^x.`

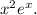
Step-by-step explanation:

To find the particular solution of the differential equation y'' - y' - 2y =
`x^2e^x,` first, determine the complementary solution, which solves the associated homogeneous equation. The characteristic equation yields roots λ = -1, 2. Consequently, the complementary solution is
`y_c(x) = C1e^(-x) + C2e^(2x).`

Following the method of variation of parameters, assume y_p(x) = u1(x)y1 + u2(x)y2, where y1 and y2 are solutions to the associated homogeneous equation, and u1(x) and u2(x) are unknown functions. Substituting y1 =
`e^(-x) and y2 = e^(2x) i`nto the formula, compute the Wronskian and determine u1(x) and u2(x).

Finally, integrate to find y_p(x), yielding y_
`p(x) = -x^2e^x`. This solution combines the homogeneous and particular solutions to satisfy the original differential equation.