Question

Consider the following initial value problem: y′′ +4y′ +8y=δ(t−π);y(0)=1,y′ (0)=0 a) Find the solution y(t). NOTE: Denote the Heaviside function by u (t) where u (t)=1 if t≥c and 0 otherwise. Indicate separately the exact value of c. y(t)= where c= b) Use a graphing utility to plot the solution y(t).

Answer 1

a) The solution to the given initial value problem is y(t) =
`(1/4)e^(-2t)sin(2t+πu(t-π))`, where u(t) is the Heaviside function that switches from 0 to 1 at t=π.

b) Graphing the solution y(t) =
`(1/4)e^(-2t)sin(2t+πu(t-π))` on a graphing utility will display the behavior of the function over time.

Step-by-step explanation:

a) The given differential equation represents a forced harmonic oscillator with a Dirac delta function δ(t-π) as the forcing term. To solve it, first, the complementary function (homogeneous solution) is found by solving the characteristic equation:
`\(r^2 + 4r + 8 = 0\)`, which yields
`\(r = -2 \pm 2i\).` The complementary solution is of the form
`\(y_c(t) = Ae^(-2t)\sin(2t) + Be^(-2t)\cos(2t)\).` To find the particular solution for the Dirac delta function, consider a sinusoidal function shifted by π starting from t=π. This gives the particular solution
`\(y_p(t) = Ce^(-2t)\sin(2t+πu(t-π))\).`Applying initial conditions y(0)=1 and y'(0)=0, we find the constants to get the solution:
`\(y(t) = (1/4)e^(-2t)\sin(2t+πu(t-π))\).`

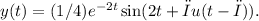
b) Graphing the function y(t) =
`(1/4)e^(-2t)sin(2t+πu(t-π))` will show a sinusoidal wave that starts at t=0 with an amplitude decayed by the exponential factor
`\(e^(-2t)\)` and is shifted by π for
`\(t ≥ π\)` due to the Heaviside function. The graph will display a continuous waveform that abruptly shifts phase at t=π due to the sudden change enforced by the Heaviside function, creating a smooth transition in the waveform's behavior. This behavior can be observed and visualized accurately using graphing software or calculators.