Question

The vector equation r (u, u) = u cosan + usinuj + uk, 0 < u < 2π, 0 < u < 1, describes a helicoid (spiral ramp). What is the surface area?

Answer 1

The surface area of the helicoid described by the vector equation
`\( \mathbf{r}(u, u)` = u cos
`(\alpha) \mathbf{i}` + u sin
`(\alpha) \mathbf{j}` + u
`\mathbf{k}` \), where (0 < u < 2
`\pi`) and (0 < u < 1), is (2
`\pi √(2)\)` square units.

Explanation:

The surface area of a helicoid is calculated using the formula for surface area of a parametric surface:

S =
`\int \int ||\mathbf{r}_u * \mathbf{r}_v|| \, du \, dv\)`

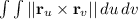
where
`\(\mathbf{r}(u, v)\)` is the parametric representation of the surface. In this case, u varies from 0 to (2
`\pi`) and v ranges from 0 to 1.

The first step involves finding the partial derivatives
`\(\mathbf{r}_u\)` and
`\(\mathbf{r}_v\)` of the vector equation
`\(\mathbf{r}(u, u)\)`. Differentiating
`\(\mathbf{r}(u, u)\)` with respect to u gives
`\(\mathbf{r}_u` = cos
`(\alpha) \mathbf{i}` + sin(
`\alpha) \mathbf{j}` +
`\mathbf{k}`), and
`\(\mathbf{r}_v\)` is simply
`\(\mathbf{k}\)`.

Next, we compute the cross product of
`\(\mathbf{r}_u\)` and
`\(\mathbf{r}_v\)` to obtain the magnitude of the cross product,
`\(||\mathbf{r}_u * \mathbf{r}_v||\)`, which simplifies to
`\(√(2)\)`.

Integrating this magnitude over the given limits of u and v, which are (0 < u < 2
`\pi`) and (0 < v < 1), yields the surface area S =
`\int_0^(2\pi) \int_0^1 √(2) \, du \, dv\)`.

The double integration simplifies to S =
`2\pi √(2)\)`, which represents the surface area of the helicoid described by the given vector equation.