Question

Solve the following equation with initial condition y(1) = 1 (4x + y)dx + (-x + y)dy = 0

Answer 1

The solution to the given initial value problem is
`\(y(x) = e^(-x)\)`.

Step-by-step explanation:

To solve the differential equation
`\((4x + y)dx + (-x + y)dy = 0\)` with the initial condition
`\(y(1) = 1\)`, we can recognize it as a first-order linear differential equation. To solve it, we can use the method of separating variables.

The given equation can be rearranged as
`\((4x + y)dx = (x - y)dy\)`. Now, separate variables by dividing both sides by
`\((4x + y)\) and \((x - y)\)`:

`\[(1)/(4x + y)dx = -(1)/(x - y)dy\]`

Now, integrate both sides separately:

`\[\int (1)/(4x + y)dx = -\int (1)/(x - y)dy\]`

This leads to
`\(\ln|4x + y| = -\ln|x - y| + C\)`, where
`\(C\)` is the constant of integration. Simplifying further, we get:

`\[\ln|4x + y| + \ln|x - y| = C\]`

Combine the logarithms using the properties of logarithms:

`\[\ln|4x + y(x)||x - y(x)|| = C\]`

Exponentiate both sides:

`\[|4x + y(x)||x - y(x)| = e^C\]`

Now, consider the initial condition
`\(y(1) = 1\)` to find the value of
`\(C\)`. Substituting
`\(x = 1\)` and
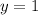`\(y = 1\)` into the equation, we get
`\(5 = e^C\)`, so
`\(C = \ln 5\)`.

Substitute
`\(C\)` back into the equation, simplify, and solve for
`\(y(x)\)` to obtain
`\(y(x) = e^(-x)\)`, which is the solution to the initial value problem.