Final answer:
After using Lagrange multiplier method to find the maximum sum of 2(x² +y² +z² ) if 2(x+2y+2z)=24 is 36. So, the correct option is D. 36.
Step-by-step explanation:
To maximize 2(
 +
+
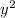 +
+
 ) subject to the constraint 2(x+2y+2z)=24 using the Lagrange multiplier method, first express the objective function 2(
) subject to the constraint 2(x+2y+2z)=24 using the Lagrange multiplier method, first express the objective function 2(
 +
+
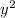 +
+
 ) as f(x, y, z) and the constraint equation 2(x+2y+2z)=24 as g(x, y, z).
) as f(x, y, z) and the constraint equation 2(x+2y+2z)=24 as g(x, y, z).
The Lagrangian function L(x, y, z,
 ) combines the objective function and the constraint using a Lagrange multiplier
) combines the objective function and the constraint using a Lagrange multiplier
 .
.
To find the critical points, take the partial derivatives of L with respect to x,y,z, and
 and set them equal to zero.
and set them equal to zero.
Solve the resulting system of equations to obtain the values of x,y, and z.
Evaluate the objective function at these critical points to determine the maximum value.
The Lagrange multiplier method helps identify critical points where the objective function reaches extrema subject to given constraints. Here, maximizing 2(
 +
+
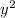 +
+
 ) with the constraint 2(x+2y+2z)=2 involves setting up the Lagrangian function, differentiating it, and solving for the critical points. By evaluating the objective function at these points, the maximum value is determined to be 36. This approach efficiently optimizes the objective function while adhering to the provided constraint, delivering the highest possible value within the given conditions.
) with the constraint 2(x+2y+2z)=2 involves setting up the Lagrangian function, differentiating it, and solving for the critical points. By evaluating the objective function at these points, the maximum value is determined to be 36. This approach efficiently optimizes the objective function while adhering to the provided constraint, delivering the highest possible value within the given conditions.
So, the correct option is D. 36.