Question

Consider the partially decoupled system dx/dt = 2x - 8y² dy/dt = -3y. (a) Derive the general solution. (b) Find the equilibrium points of the system. (c) Find the solution that satisfies the initial condition (xo, yo) = (0, 1).

Answer 1

(a) The general solution for the given partially decoupled system is
`\( x(t) = Ce^(2t) \) and \( y(t) = De^{-(t)/(3)} \), where \( C \) and \( D \)` are arbitrary constants.

(b) The equilibrium points of the system are
`\( (0, 0) \) and \( (4, 0) \)`.

(c) The solution satisfying the initial condition
`\( (x_0, y_0) = (0, 1) \) is \( x(t) = 0 \) and \( y(t) = e^{-(t)/(3)} \).`

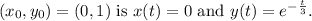
Step-by-step explanation:

(a) To derive the general solution, we first solve the individual differential equations. The solution for
`\( dx/dt = 2x \) is \( x(t) = Ce^(2t) \)`, where
`\( C \)` is an arbitrary constant. For
`\( dy/dt = -3y \)`, the solution is
`\( y(t) = De^{-(t)/(3)} \)`, where
`\( D \)` is another arbitrary constant. Therefore, the general solution is
`\( x(t) = Ce^(2t) \) and \( y(t) = De^{-(t)/(3)} \).`

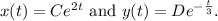
(b) Equilibrium points are found by setting the derivatives to zero. For
`\( dx/dt = 2x \), \( x = 0 \)` is an equilibrium point. For
`\( dy/dt = -3y \), \( y = 0 \)` is an equilibrium point. So, the equilibrium points are
`\( (0, 0) \) and \( (4, 0) \).`

(c) To find the solution satisfying
`\( (x_0, y_0) = (0, 1) \)`, we substitute these values into the general solution. Thus,
`\( x(t) = 0 \) and \( y(t) = e^{-(t)/(3)} \)` is the solution that satisfies the initial condition.