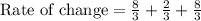Final Answer:
The gradient vector of
 is (2x, 2y, -4) . The direction of maximum increase at the point P(2, -1, 1) is
is (2x, 2y, -4) . The direction of maximum increase at the point P(2, -1, 1) is
 . The rate of change of f at P in the direction of
. The rate of change of f at P in the direction of
 is 6.
is 6.
Step-by-step explanation:
To solve this problem, we'll go through each part step by step.
a) Find the gradient vector of
 :
:
The gradient vector
 is a vector containing the partial derivatives of f with respect to each variable. In this case:
is a vector containing the partial derivatives of f with respect to each variable. In this case:
![\[ \\abla f = \left( (\partial f)/(\partial x), (\partial f)/(\partial y), (\partial f)/(\partial z) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/tyizch0edg9hxsp2gnzfqpe6e3ohs74gyo.png)
So, let's find the partial derivatives:
![\[ (\partial f)/(\partial x) = 2x \]](https://img.qammunity.org/2024/formulas/mathematics/college/toq0ygpjlayuxxelycp7i9dum6b30c3xgj.png)
![\[ (\partial f)/(\partial y) = 2y \]](https://img.qammunity.org/2024/formulas/mathematics/college/h0ptkukwp7xjc1v4hwo7pw65zg2lqisogl.png)
![\[ (\partial f)/(\partial z) = -4 \]](https://img.qammunity.org/2024/formulas/mathematics/college/l34o6fwnc2r795ntz95p5k4rryukzeii7n.png)
Therefore, the gradient vector
 is (2x, 2y, -4).
is (2x, 2y, -4).
b) Find the direction of maximum increase at P(2, -1, 1):
To find the direction of maximum increase, we use the gradient vector. The direction of maximum increase is the direction of the gradient vector. At the point
 , the gradient vector is
, the gradient vector is
 .
.
So, the direction of maximum increase at P is
 , where
, where
 is the magnitude of the gradient vector.
is the magnitude of the gradient vector.
![\[ |\\abla f| = √(4^2 + (-2)^2 + (-4)^2) = √(16 + 4 + 16) = √(36) = 6 \]](https://img.qammunity.org/2024/formulas/mathematics/college/eja71ghpct4qanxyuzdxpvoar7x9j20u63.png)
![\[ \mathbf{u} = \left( (4)/(6), (-2)/(6), (-4)/(6) \right) = \left( (2)/(3), (-1)/(3), (-2)/(3) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/pg814beq63u3atz6pwl1drpci3c7afiq10.png)
So, the direction of maximum increase at P is
 .
.
c) Find the rate of change of f at P in the direction of
 :
:
The rate of change of f at P in the direction of
 is given by the dot product of the gradient vector and the unit vector
is given by the dot product of the gradient vector and the unit vector
 .
.
![\[ \text{Rate of change} = \\abla f \cdot \mathbf{u} \]](https://img.qammunity.org/2024/formulas/mathematics/college/toa5tl54u9xshnzx7yuo3bdr5vhvndwclh.png)
![\[ \text{Rate of change} = (4, -2, -4) \cdot \left( (2)/(3), (-1)/(3), (-2)/(3) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/kgwdn1sgluxg08k53qjv949rxb6iyuxo5p.png)