Final Answer:
 This solution represents the combination of sinusoidal functions that satisfy the given initial value problem.
This solution represents the combination of sinusoidal functions that satisfy the given initial value problem.
Explanation:
To solve the given initial value problem using Laplace transforms, first, we apply the Laplace transform to the differential equation
 and the initial conditions
and the initial conditions
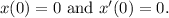
After rearranging and applying the initial conditions, we derive the transformed equation in terms of the Laplace variable
 which gives us the equation in terms of
which gives us the equation in terms of
 yields a partial fraction decomposition.
yields a partial fraction decomposition.
Through inverse Laplace transform and using trigonometric identities, the solution
 can be expressed as a combination of sine functions with different frequencies, amplitudes, and phase shifts, corresponding to the coefficients obtained from the partial fraction decomposition.
can be expressed as a combination of sine functions with different frequencies, amplitudes, and phase shifts, corresponding to the coefficients obtained from the partial fraction decomposition.
The final solution for
 This solution represents the combination of sinusoidal functions that satisfy the given initial value problem.
This solution represents the combination of sinusoidal functions that satisfy the given initial value problem.