Final Answer:
The Fourier series of
 on the interval
on the interval
 is challenging to express analytically due to the complexity of the integrals involved. Numerical methods or specialized software may be required to evaluate the coefficients. Once obtained, the Fourier series representation can be written as a sum of cosines and sines over the specified interval.
is challenging to express analytically due to the complexity of the integrals involved. Numerical methods or specialized software may be required to evaluate the coefficients. Once obtained, the Fourier series representation can be written as a sum of cosines and sines over the specified interval.
Step-by-step explanation:
To find the Fourier series of the function
 , we need to express it as a periodic function over a specified interval. The Fourier series representation of a periodic function
, we need to express it as a periodic function over a specified interval. The Fourier series representation of a periodic function
 on the interval
on the interval
![\([-L, L]\)](https://img.qammunity.org/2024/formulas/mathematics/college/lq73d0yj5ht6jj3vnn9ot1cjr91titb1fv.png) is given by:
is given by:
![\[ f(x) = a_0 + \sum_(n=1)^(\infty) \left[ a_n \cos\left((2n\pi x)/(T)\right) + b_n \sin\left((2n\pi x)/(T)\right) \right] \]](https://img.qammunity.org/2024/formulas/mathematics/college/brc05xvswwd08g19dew5uy0w41ebyybsqb.png)
where
 is the period of the function.
is the period of the function.
In this case,
 is defined on the interval
is defined on the interval
 because
because
 cannot be zero. Therefore, the period T is
cannot be zero. Therefore, the period T is
 .
.
Now, let's find the coefficients
 and
and
 using the following formulas:
using the following formulas:
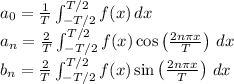
For
 :
:
![\[ a_0 = (1)/(2/3) \int_(-1/3)^(1/3) (1)/(1 + 9x^2) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/college/7q3i2ietl4ltie7bsnft3v4zz3x9z76e65.png)
For
 :
:
![\[ a_n = (2)/(2/3) \int_(-1/3)^(1/3) (1)/(1 + 9x^2) \cos\left((2n\pi x)/(2/3)\right) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/college/omoo2hjy011sf64a6j06q8g9nfw9bpa6v7.png)
For
 :
:
![\[ b_n = (2)/(2/3) \int_(-1/3)^(1/3) (1)/(1 + 9x^2) \sin\left((2n\pi x)/(2/3)\right) \,dx \]](https://img.qammunity.org/2024/formulas/mathematics/college/jkdish7ia54c723yqld584nbcj0lkl9rux.png)
These integrals may require techniques such as partial fraction decomposition and trigonometric substitutions. Unfortunately, solving these integrals explicitly for the given function may be challenging, and numerical methods or specialized software may be needed to evaluate them.
Once you find the coefficients, you can substitute them into the Fourier series formula to obtain the representation of f(x) as a sum of sines and cosines.