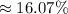Question

Consider two waves yi(x, t) and y2(r, t) that are identical except for a phase shift propagating in the same medium. (a)What is the phase shift, in radians, if the amplitude of the resulting wave is 1.75 times the amplitude of the individual waves? (b) What is the phase shift in degrees? (c) What is the phase shift as a percentage of the individual wavelength?

Answer 1

A. Phase shift
`\( \phi = 1.01 \)` radians

B. Phase shift
`\( \phi \approx 57.9^\circ \)`

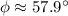
C. Phase shift as a percentage of the individual wavelength
`\( \approx 16.07\% \)`

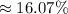
How to determine this?

Given:
`\( A\pi\omega = 2A \cos((\phi)/(2)) \)`

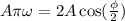
Given that the amplitude of the resulting wave is
`\( 1.7A \)`, we can write:

`\( 1.7A = 2A \cos((\phi)/(2)) \)`

Solving for
`\( \phi \)`:

`\( \cos((\phi)/(2)) = (1.7)/(2) \)`

`\( (\phi)/(2) = \cos^(-1)\left((1.7)/(2)\right) \)`

`\( \phi = 2 * \cos^(-1)\left((1.7)/(2)\right) \)`

`\( \phi = 1.01 \) radians`

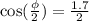
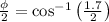
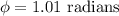
For converting radians to degrees:

`\( \phi = 1.01 \) radians \( = 1.01 * (180)/(\pi) \) degrees \( \approx 57.9^\circ \)`

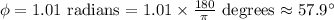
Now, for the percentage of the phase shift compared to the individual wavelength:

`\( (\phi)/(2\Lambda) * 100 = (1.01)/(2\Lambda) * 100 = 16.07\% \)`

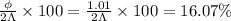
Hence:

A. Phase shift
`\( \phi = 1.01 \)` radians

B. Phase shift
`\( \phi \approx 57.9^\circ \)`

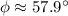
C. Phase shift as a percentage of the individual wavelength
`\( \approx 16.07\% \)`