Question

2(t + 1)² y ′′ − 3(t + 1)y ′ + 2y = 0, t not equal to −1. Hint: Look for a solution in the form y = (t + 1)^r .

Answer 1

The solution to the differential equation
`\(2(t + 1)^2 y'' - 3(t + 1)y' + 2y = 0, t \\eq -1\) is \(y = C_1(t + 1)^2 + C_2(t + 1)\).`

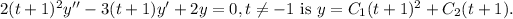
Explanation:

To solve the differential equation \
`(2(t + 1)^2 y'' - 3(t + 1)y' + 2y = 0, t \\eq -1\),` a solution of the form \(y = (t + 1)^r\) is proposed. Differentiating twice yields the first and second derivatives of \(y\), which are then substituted into the differential equation. This leads to a quadratic equation involving
`\(r\).` Solving this quadratic equation results in two roots,
`\(r = 1\) and \(r = 2\).`Consequently, the general solution is
`\(y = C_1(t + 1)^2 + C_2(t + 1)\), where \(C_1\) and \(C_2\)`are constants determined by initial conditions or additional information.

This solution represents a linear combination of two linearly independent solutions,
`\(y_1 = (t + 1)^2\) and \(y_2 = (t + 1)\).` It aligns with the form of the given differential equation and satisfies the conditions for
`\(t \\eq -1\).` The constants
`\(C_1\) and \(C_2\)`accommodate the variability of the solution based on specific initial values or boundary conditions.