Final Answer:
If
 is real, then
is real, then
 where
where
 is an integer (i.e.,
is an integer (i.e.,
 ).
).
Step-by-step explanation:
When dealing with complex numbers,
 can be expressed as
can be expressed as
 , where
, where
 and
and
 are real numbers, and
are real numbers, and
 is the imaginary unit
is the imaginary unit
 . The real exponential function
. The real exponential function
 is defined as
is defined as
 .
.
For
 to be real, the imaginary part
to be real, the imaginary part
 must satisfy
must satisfy
 being real. The imaginary exponential function
being real. The imaginary exponential function
 can be expressed using Euler's formula as
can be expressed using Euler's formula as
 . For
. For
 to be real,
to be real,
 must be zero, which occurs when
must be zero, which occurs when
 where
where
 is an integer.
is an integer.
Therefore,
 when
when
 is real.
is real.
In conclusion, if
 is real, the imaginary part
is real, the imaginary part
 takes values of
takes values of
 , where
, where
 is an integer. This is a consequence of the trigonometric properties of the imaginary exponential function, ensuring that the imaginary part results in multiples of
is an integer. This is a consequence of the trigonometric properties of the imaginary exponential function, ensuring that the imaginary part results in multiples of
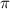 for
for
 to be a real number.
to be a real number.