Question

Which equation could be used to find the area, A , of square R ? 3 squares. The left square is labeled R. The right square is 12 by 12. The top square is 6 by 6. There is a right triangle in the center of the squares.

Answer 1

The equation to find the area (A) of square R is
`\(A = (12 - 6)^2\)`.

Step-by-step explanation:

To determine the area of square R, we need to consider the difference in the side lengths of the larger squares. The right square has a side length of 12, and the top square has a side length of 6. The portion of square R not covered by the smaller square is the difference in their side lengths, which is 12 - 6 = 6. Squaring this difference gives the area of the square
`\(R\): \(A = (12 - 6)^2 = 6^2 = 36\).`

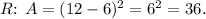
The reason for subtracting the side length of the top square from the side length of the right square is that the overlapping region forms a right-angled triangle in the center of squares R. By finding the difference in side lengths, we are essentially finding the length of the legs of this right triangle. Squaring this value gives the area of square R, which represents the remaining uncovered portion.

Understanding how to derive the equation for the area of square R is crucial for solving geometric problems involving overlapping shapes. In this case, recognizing the geometric configuration and using the difference in side lengths allows us to formulate an equation that accurately represents the area of square R.