Question

Part (a): List the first six terms of this sequence.

Answer 1

a. The first six terms of the sequence defined by aₙ = n/(2n + 1) are:

a₁ = 1/3, a₂ = 2/5, a₃ = 3/7, a₄ = 4/9, a₅ = 5/11, a₆ = 6/13.

b. The sequence appears to approach a limit, which is L = 1/2, as n approaches infinity.

Step-by-step explanation:

Given the sequence aₙ = n/(2n + 1), we're asked to find the first six terms and determine whether the sequence appears to have a limit as n approaches infinity.

a. Finding the first six terms:

Plug in \(n = 1, 2, 3, 4, 5, 6\) into the formula aₙ = n/(2n + 1) to calculate the terms of the sequence.

a₁ ={1}/(2(1) + 1) = 1/3

a₂ = {2}/(2(2) + 1) = 2/5

a₃ = {3}/(2(3) + 1) = 3/7

a₄ = {4}/(2(4) + 1) = 9/4

a₅ = {5}/(2(5) + 1) = 5/11

a₆ = {6}/(2(6) + 1) = 6/13

Therefore, the first six terms of the sequence are a₁ = 1/3, a₂ = 2/5, a₃ = 3/7, a₄ = 4/9, a₅ = 5/11, a₆ = 6/13.

b. Observing the behavior and finding the limit:

From the calculated terms, it appears that as \(n\) increases, the terms of the sequence are getting closer to a particular value.

To determine the limit as n approaches infinity, express the limit of the sequence mathematically:

`\(\lim_(n \to \infty) a_n = \lim_(n \to \infty) (n)/(2n + 1)\).`

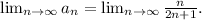
By dividing the highest power of \(n\) in the numerator and denominator, you get:

`\(\lim_(n \to \infty) (n)/(2n + 1) = \lim_(n \to \infty) (1)/(2 + (1)/(n)) = (1)/(2)\).`

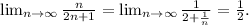
This demonstrates that as \(n\) approaches infinity, the terms of the sequence aₙ = n/(2n + 1) converge towards the limit L = 1/2

By systematically calculating the terms of the sequence for specific values of \(n\) and then applying the concept of limits to the sequence formula, we determined that the sequence converges to a limit of 1/2 as (n) approaches infinity.

Complete Question

a. List the first six terms of the sequence defined by aₙ = n/(2n + 1).

b. Does the sequence have a limit? what is is?