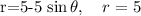Question

Find the area of the region that lies inside the first curve and outside the second curve. r=5-5\sinθ, r=5.

Answer 1

The area of the region that lies inside the first curve and outside the second curve is
`$(\pi)/(2)$` square units.

To find the area of the region that lies inside the first curve
`$r = 5 - 5\sin(\theta)$` and outside the second curve r = 5, you can use the following steps:

1. Determine the limits of integration for θ:

To find the area between two polar curves, you need to determine the values of θ where the two curves intersect. In this case, the curves intersect when
`$r = 5 - 5\sin(\theta)$` equals r = 5.

This happens when
`$5 - 5\sin(\theta) = 5$`, so
`$\sin(\theta) = 0$`. You can find the values of θ for which this occurs in the interval [0, 2π] since we want a complete loop:

`$\sin (\theta)=0 \Longrightarrow \theta=0, \pi, 2 \pi$`.

So, your limits of integration for θ are 0 to 2π.

2. Set up the integral for the area:

The area between two polar curves can be calculated using the following integral formula:

`Area =(1)/(2) \int_(\theta_1)^(\theta_2)\left[r_1(\theta)^2-r_2(\theta)^2\right] d \theta$`

where

• 
  `$r_1(\theta)$` is the outer curve (in this case,
  `$r_1(\theta)`) =
  `5 - 5\sin(\theta)$)`.
• 
  `$r_2(\theta)$` is the inner curve (in this case,
  `$r_2(\theta) = 5$`).
• 
  `$\theta_1$` and
  `$\theta_2$` are the limits of integration (in this case, 0 and 2π).

Substituting these values into the formula:

`Area =(1)/(2) \int_0^(2 \pi)\left[(5-5 \sin (\theta))^2-5^2\right] d \theta$`

3. Simplify the integrand:

Expand and simplify the integrand:

`$$ \begin{align*} \text{Area} &= (1)/(2) \int_(0)^(2\pi) [(25 - 50\sin(\theta) + 25\sin^2(\theta)) - 25] d\theta \\ &= (1)/(2) \int_(0)^(2\pi) (-50\sin(\theta) + 25\sin^2(\theta)) d\theta. \end{align*} $$`

4. Integrate:

Now, integrate the simplified expression with respect to θ:

`$$ \text{Area} = (1)/(2) \left[-50\int_(0)^(2\pi)\sin(\theta)d\theta + 25\int_(0)^(2\pi)\sin^2(\theta)d\theta\right]. $$`

For the first integral,
`$\int_(0)^(2\pi)\sin(\theta)d\theta$`, you can see that it integrates to 0 over a full period of sine, so it's equal to 0.

For the second integral,
`$\int_(0)^(2\pi)\sin^2(\theta)d\theta$`, you can use the identity
`$\sin^2(\theta) = (1)/(2)(1 - \cos(2\theta))$`:

`$\begin{aligned} \text { Area } & =(1)/(2)\left[0+25 \int_0^(2 \pi) (1)/(2)(1-\cos (2 \theta)) d \theta\right] \\ & =(1)/(4) \int_0^(2 \pi)(1-\cos (2 \theta)) d \theta\end{aligned}$`

Now, integrate term by term:

`$\begin{aligned} \text { Area } & =(1)/(4)\left[\int_0^(2 \pi) 1 d \theta-\int_0^(2 \pi) \cos (2 \theta) d \theta\right] \\ & =(1)/(4)\left[[\theta]_0^(2 \pi)-\left[(1)/(2) \sin (2 \theta)\right]_0^(2 \pi)\right] \\ & =(1)/(4)[2 \pi-0] \\ & =(1)/(4)(2 \pi) \\ & =(\pi)/(2) .\end{aligned}$`

So, the answer is
`$(\pi)/(2)$` square units.

The complete question is here:

Find the area of the region that lies inside the first curve and outside the second curve.

`$$r=5-5 \sin \theta, \quad r=5$$`