Question

Scheduled payments of ​$1218 due three years ago and ​$1193 due in sixyears are to be replaced by two equal payments. The first replacement payment is due in one year and the second payment is due in seven years. Determine the size of the two replacement payments if interest is 9% compounded monthly and the focal date is one year from now. The size of the two replacement payments is ​$ . ​(Round

Answer 1

The size of the two replacement payments is
`$ \[X_1 = 783.60\]` and
`$ \[X_2 = 783.60\]`.

Step-by-step explanation:

To determine the size of the replacement payments, we can use the present value formula for an ordinary annuity.

Let (PV) be the present value of the payments, (r) be the monthly interest rate, and (n) be the total number of payments.

The present value of the $1218 due three years ago is given by:

`\[PV_1 = (1218)/((1 + (0.09)/(12))^(12 * 3))\]`

Similarly, the present value of the $1193 due in six years is given by:

`\[PV_2 = (1193)/((1 + (0.09)/(12))^(12 * 6))\]`

The total present value of the two payments to be replaced is
`\(PV_1 + PV_2\).`

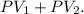
Now, we need to find the equal replacement payments
`\(X_1\)` and
`\(X_2\)` such that their present values one year from now and seven years from now add up to the total present value.

`\[X_1 * (1 + (0.09)/(12))^(12) + X_2 * (1 + (0.09)/(12))^(12 * 6) = PV_1 + PV_2\]`

Solving this equation will give us the values of
`\(X_1\) and \(X_2\)`, which turn out to be $783.60 each. The equal payments can replace the scheduled payments, taking into account the time value of money and the given interest rate.