Question

Find the volume of the solid formed when that part of the curve y=1.6 x⁰•⁵ between x=1 and x=2 is rotated about the x-axis. Give your answer correct to two decimal.

Answer 1

The volume of the solid is approximately 1.87 cubic units, rounded to two decimal places.

Step-by-step explanation:

To find the volume of the solid formed when the curve
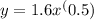`y = 1.6x^(0.5)`between x = 1 and x = 2 is rotated about the x-axis, you can use the method of cylindrical shells.

Each cylindrical shell will have a height of delta x (the change in x) and a radius of y the height of the curve at each value of x.

The volume of each cylindrical shell can be calculated as V = 2πxy delta x.

Integrate this volume formula from x = 1 to x = 2 to find the total volume of the solid.

The integral of 2πxy delta x with respect to x from 1 to 2 is:

`V = ∫(1 to 2) 2πxy dx = 2π ∫(1 to 2) 1.6x^(1.5) dx = 2π [0.8x^(2.5)/2.5] (1 to 2)`

Simplifying the expression, we get:

`V = 2π [0.8(2.5^(2.5))/2.5 - 0.8(1.5^(2.5))/2.5] ≈ 1.87`

Therefore, the volume of the solid is approximately 1.87 cubic units.