Final Answer:
The equation representing the solution to John Bernoulli's differential equation is
 is an arbitrary constant and
is an arbitrary constant and
 is a parameter.
is a parameter.
Step-by-step explanation:
John Bernoulli's differential equation,
![\( y[1 + (dy/dx)^2] = c \)](https://img.qammunity.org/2024/formulas/mathematics/college/ve0wxm0zdtl5tsppqwwrn7bkjhlw6gklou.png) , is a first-order nonlinear ordinary differential equation. To find the solution, we can use the substitution
, is a first-order nonlinear ordinary differential equation. To find the solution, we can use the substitution
 is a parameter. This transforms the differential equation into a separable one.
is a parameter. This transforms the differential equation into a separable one.
Integrating with respect to
 is an arbitrary constant. To find
is an arbitrary constant. To find
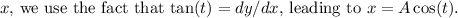
The solution represents parametric equations for the curve. As
 varies, the corresponding values of
varies, the corresponding values of
 trace the curve determined by the given differential equation. The arbitrary constant
trace the curve determined by the given differential equation. The arbitrary constant
 allows for different parameterizations of the curve. This solution provides insight into the relationship between
allows for different parameterizations of the curve. This solution provides insight into the relationship between
 that satisfies the given differential equation.
that satisfies the given differential equation.