Final Answer
The frequency ω for the particular solution to the given differential equation to have the largest amplitude is ω = √(2/3).
Step-by-step explanation
To find the frequency ω that maximizes the amplitude of the particular solution, we'll start by assuming the particular solution takes the form A * e^(iωt). Substituting this into the given differential equation, we get:
![\[3 (d²y)/(dt²) + (dy)/(dt) + 2y = e^(iωt)\]](https://img.qammunity.org/2024/formulas/mathematics/college/6hdtdduzmejnhb933nn8ayd22vgnrvwhi5.png)
Replace
 into the equation:
into the equation:
![\[3iω(3Aiωe^(iωt)) + iω(Ae^(iωt)) + 2Ae^(iωt) = e^(iωt)\]](https://img.qammunity.org/2024/formulas/mathematics/college/irf13i4jh4xlfxo3uoiyv771nltcqcaeyv.png)
Simplify by dividing through by
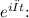
![\[3iω(3Aiω) + iω(A) + 2A = 1\]](https://img.qammunity.org/2024/formulas/mathematics/college/vxsww4gofp6imen9m7ojz9yizvm3o0p3q8.png)
Solving for A:
![\[9ω²Ai + ωAi + 2A = 1\]](https://img.qammunity.org/2024/formulas/mathematics/college/bamwkrbmc1vtpcsv629ng6fncd54l80md4.png)
![\[A(9ω²i + ωi + 2) = 1\]](https://img.qammunity.org/2024/formulas/mathematics/college/d88irlz905zyi66bf2ay2kit2hj9n1ddr2.png)
![\[A = (1)/(9ω²i + ωi + 2)\]](https://img.qammunity.org/2024/formulas/mathematics/college/f1a2fs44fajeswj93unbx0wsq2mronpkvh.png)
We want to maximize the amplitude, which is the modulus of A. The amplitude is maximized when the denominator
 is minimized. To minimize the modulus of the denominator, consider the denominator's square:
is minimized. To minimize the modulus of the denominator, consider the denominator's square:
![\[(9ω²i + ωi + 2)(9ω²i + ωi + 2)^* = |9ω²i + ωi + 2|^2\]](https://img.qammunity.org/2024/formulas/mathematics/college/y2ksvur4zbv55dtcj7bpdznsweyke8l9rp.png)
Where
 denotes the complex conjugate. The denominator's square becomes:
denotes the complex conjugate. The denominator's square becomes:
![\[81ω^4 + 18ω² + 4\]](https://img.qammunity.org/2024/formulas/mathematics/college/w5cbjjhm7rbsdrncvybdhehtxlrfu61n3t.png)
To minimize this expression, take its derivative with respect to ω and set it to zero:
![\[(d)/(dω)(81ω^4 + 18ω² + 4) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/college/8vibf35aokhujm79qzaxhf4e7a6lbflmeo.png)
![\[324ω^3 + 36ω = 0\]](https://img.qammunity.org/2024/formulas/mathematics/college/l3va4evwrwgew0rg2zu8xsnkl04wbo637g.png)
![\[ω(9ω² + 1) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/college/mg7es2qe0u7sq7a7bqogsamcuf0yb2iouz.png)
Solving for ω, we get
 which is the frequency that maximizes the amplitude of the particular solution.
which is the frequency that maximizes the amplitude of the particular solution.