Final Answer:
To find
 substitute the expressions for f(x) and g(x) into the fraction. Therefore,
substitute the expressions for f(x) and g(x) into the fraction. Therefore,
 becomes
becomes
 . This is the final simplified expression for
. This is the final simplified expression for
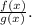
![\[ (f(x))/(g(x)) = (x^2 - x - 2)/(x - 2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5w0sp9p1lbvpl208yeqk0f2y9fk0ti72vj.png)
Step-by-step explanation:
To find
 substitute the expressions for f(x) and g(x) into the fraction. Therefore,
substitute the expressions for f(x) and g(x) into the fraction. Therefore,
 becomes
becomes
 . This is the final simplified expression for
. This is the final simplified expression for
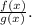
Now, let's break down the steps for clarity. Start by substituting
 and g(x) = x - ) into the fraction:
and g(x) = x - ) into the fraction:
![\[ (f(x))/(g(x)) = (x^2 - x - 2)/(x - 2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5w0sp9p1lbvpl208yeqk0f2y9fk0ti72vj.png)
To simplify this expression, factor the numerator:
![\[ ((x + 1)(x - 2))/(x - 2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/b3yxwg9qlnu6gvttlw06em20lwygcqpd6r.png)
Now, cancel out the common factor x - 2) in the numerator and denominator:
x + 1
So,
 simplifies to x + 1. This is the simplified form of the given expression.
simplifies to x + 1. This is the simplified form of the given expression.
In summary, the simplified expression for
 . The process involves substituting the given functions into the fraction, factoring the numerator, and canceling out common factors to reach the final simplified form.
. The process involves substituting the given functions into the fraction, factoring the numerator, and canceling out common factors to reach the final simplified form.