Question

The profit y (in dollars) for a business from selling x coats is represented by y=51x. Graph the equation

Answer 1

The equation
`\(y = 51x\)` represents a linear relationship where the profit
`(\(y\))` in dollars is directly proportional to the number of coats sold
`(\(x\))`, with a constant rate of
`\(51\)` dollars per coat.

Step-by-step explanation:

The equation is in the form
`\(y = mx\)`, where
`\(m\)` is the slope of the line. In this case, the slope
`(\(m\))` is
`\(51\),` indicating that for every additional coat sold
`(\(x\))`, the profit
`(\(y\))` increases by
`\(51\)` dollars. The y-intercept is
`\(0\)` (when
`\(x = 0\))`, meaning that if no coats are sold, the profit is zero.

To graph the equation, we can choose several values for \(x\), plug them into the equation, and find the corresponding \(y\) values. For example:

When
`\(x = 1\), \(y = 51 * 1 = 51\)`

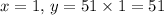
When
`\(x = 2\), \(y = 51 * 2 = 102\)`

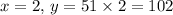
When
`\(x = 3\), \(y = 51 * 3 = 153\)`

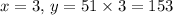
Plotting these points on a coordinate system and connecting them will yield a straight line passing through the origin (0,0) with a slope of
`\(51\).`This line represents the relationship between the number of coats sold and the corresponding profit.

In summary, the linear equation
`\(y = 51x\)` and its graph provide a clear and intuitive representation of the business's profit as it increases at a constant rate for each additional coat sold.