Main Answer:
1.
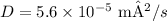
2.

3. 1.11 mm
4.
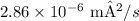
5.
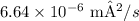
6. Your Score = X/100
Step-by-step explanation:
1. To calculate the diffusion coefficient (D) at Temperature 1, use the given formula
 , where
, where
 is the pre-exponential factor,
is the pre-exponential factor,
 is the activation energy, R is the gas constant, and T is the absolute temperature in Kelvin.
is the activation energy, R is the gas constant, and T is the absolute temperature in Kelvin.
2. For the purification of hydrogen through a palladium sheet, use Fick's first law of diffusion
 , where F is the diffusion flux, A is the area,
, where F is the diffusion flux, A is the area,
 is the concentration difference, and
is the concentration difference, and
 is the thickness of the sheet.
is the thickness of the sheet.
3. To find how far into the steel sheet the concentration is 2.5 kg/m³, use the equation for steady-state diffusion in a linear concentration profile:
 , where x is the distance into the sheet.
, where x is the distance into the sheet.
4. For the diffusion coefficient of carbon in alpha-iron (BCC) at Temperature 2, use the same formula as in Problem 1, but with the given values for Temperature 2.
5. Similarly, for the diffusion coefficient of carbon in gamma-iron (FCC) at Temperature 2, apply the formula used in Problem 4 with the relevant values.
Ensure accurate unit conversions and calculations for each problem to obtain precise engineering notation answers.