Final Answer:
The perimeter of the quadrilateral in terms of
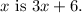
Step-by-step explanation:
To determine the perimeter of the given quadrilateral, sum the lengths of its four sides:
1.
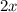
2.

3.
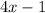
4.

Adding these side lengths:
![\[2x + (x + 3) + (4x - 1) + (x + 4) = 8x + 6.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kjd5788vba4xllsf4m9w78uuemxqwqzarj.png)
To simplify further, factor out \(2\) from both terms:
![\[2(4x + 3).\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/99b3t4lkc9ue2wez9a3v9eqny15e0yhrmj.png)
Express it in the desired format
 by factoring out
by factoring out
 from
from
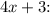
![\[2(4x + 3) = 2 \cdot 1 \cdot (4x + 3) = 1 \cdot (4x + 3).\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tac73z8ctn7cd0yozmnyu33dmasg5aw5mc.png)
Therefore, the final expression for the perimeter in terms of
 is
is
 and the correct option is D.
and the correct option is D.